Options is a highly volatile instruments among many financial instruments in the market. The premium of the options is influenced by various forces. These forces are simply called “The Option Greeks”. To be successful in options trading, traders must find out how these forces influence the option contract’s price. Options Greeks plays a crucial role in the risk and potential profitability of traders.
What are Option Greeks?

Option Greeks are a set of key metrics that help traders understand and measure how various factors influence the price of an option. These factors include changes in the underlying asset’s price, time decay, volatility, and interest rates. The Greeks are essential for assessing the risk and potential reward of an options position, and they guide traders in making more informed decisions when managing their trades.
The five primary Option Greeks are:
Delta (Δ) – Measures the sensitivity of an option’s price to changes in the price of the underlying asset.
Gamma (Γ) – Measures the rate of change of Delta as the price of the underlying asset changes.
Theta (Θ) – Measures the rate at which an option’s price decays as time passes, known as “time decay.”
Vega (V) – Measures the sensitivity of an option’s price to changes in the volatility of the underlying asset.
Rho (ρ) – Measures the sensitivity of an option’s price to changes in interest rates.
These Greeks help traders evaluate how an option’s value might change in response to movements in the market. Understanding Option Greeks is crucial for managing risk, developing strategies, and maximizing the profitability of options trades.
For example, if you hold an option position, Delta tells you how much the option’s price will change with a ₹1 movement in the underlying asset. Look at the data of Nifty Index option chain for expiry November 21st, 2024. The delta for the strike price is ….. That means if there is 1 point movement in the Nifty spot, this nifty option contract premium will move …….
Likewise, all the Greeks are analyzed to predict the possible change in premium in the near future. Now, we will discuss each option Greek in detail below.
What is Delta in Option Greeks :
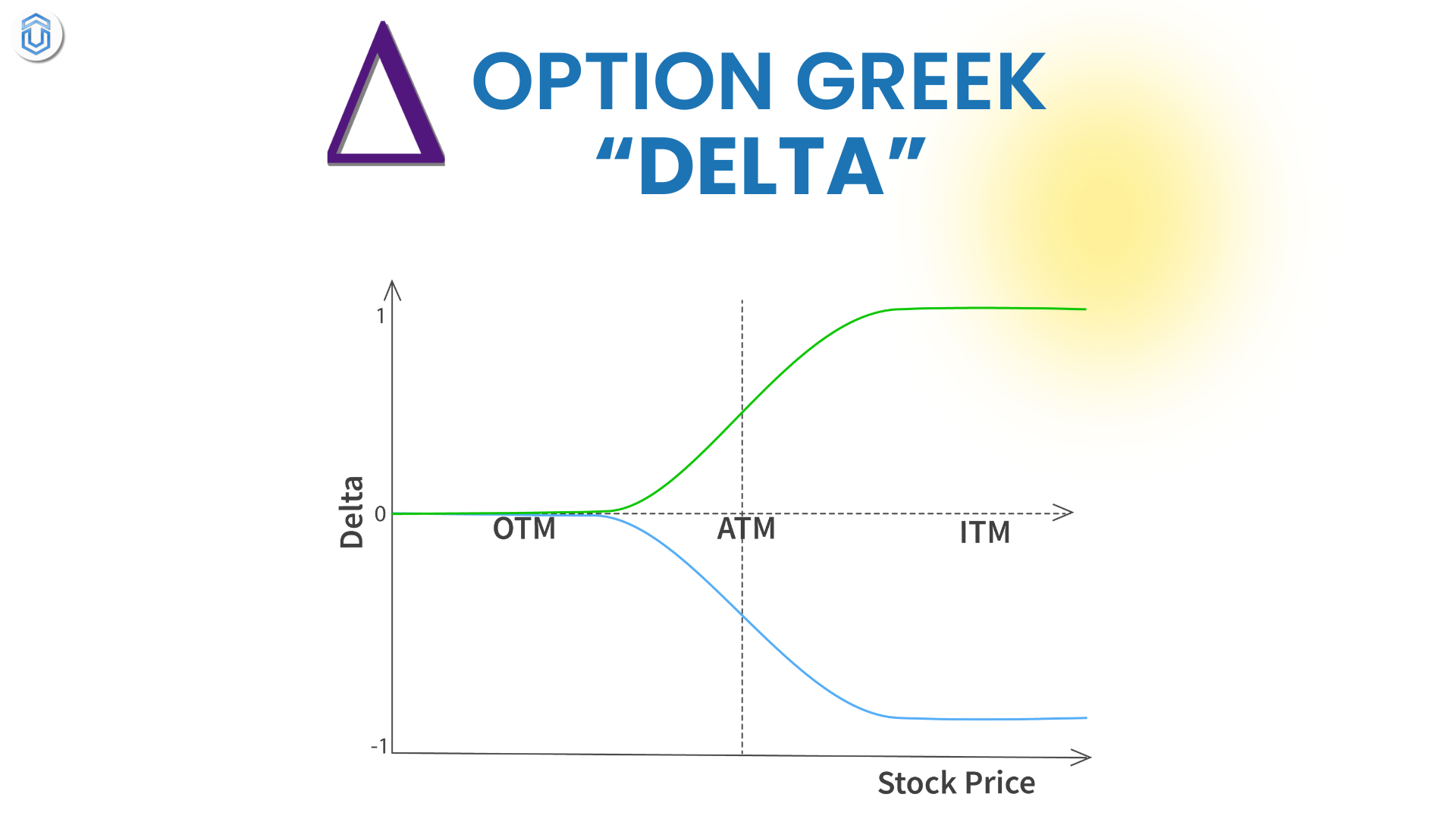
Delta is one of the most important Option Greeks and represents the sensitivity of an option’s price to changes in the price of the underlying asset. In simpler terms, Delta tells you how much the price of an option is expected to change for every movement in the underlying asset’s price.
Delta value ranges from 0 to +1 for call options and from 0 to -1 for put options.
Call Option: For a call option (the right to buy the underlying asset), Delta ranges from 0 to +1. A higher delta (closer to 1) means the option’s price is more sensitive to the price movement of the underlying asset.
Put Option: For a put option (the right to sell the underlying asset), Delta ranges from 0 to -1. A higher negative delta (closer to -1) indicates a stronger sensitivity to price changes in the underlying asset.
Example:
If a call option has a delta of 0.50, for example, this means that if the underlying asset’s price increases by ₹1, the call option’s price will increase by ₹0.50 (assuming all other factors remain constant).
Similarly, if a put option has a delta of -0.50, for every ₹1 decline in the underlying asset’s price, the price of the put option would increase by ₹0.50.
What is Gamma in Option Greeks:
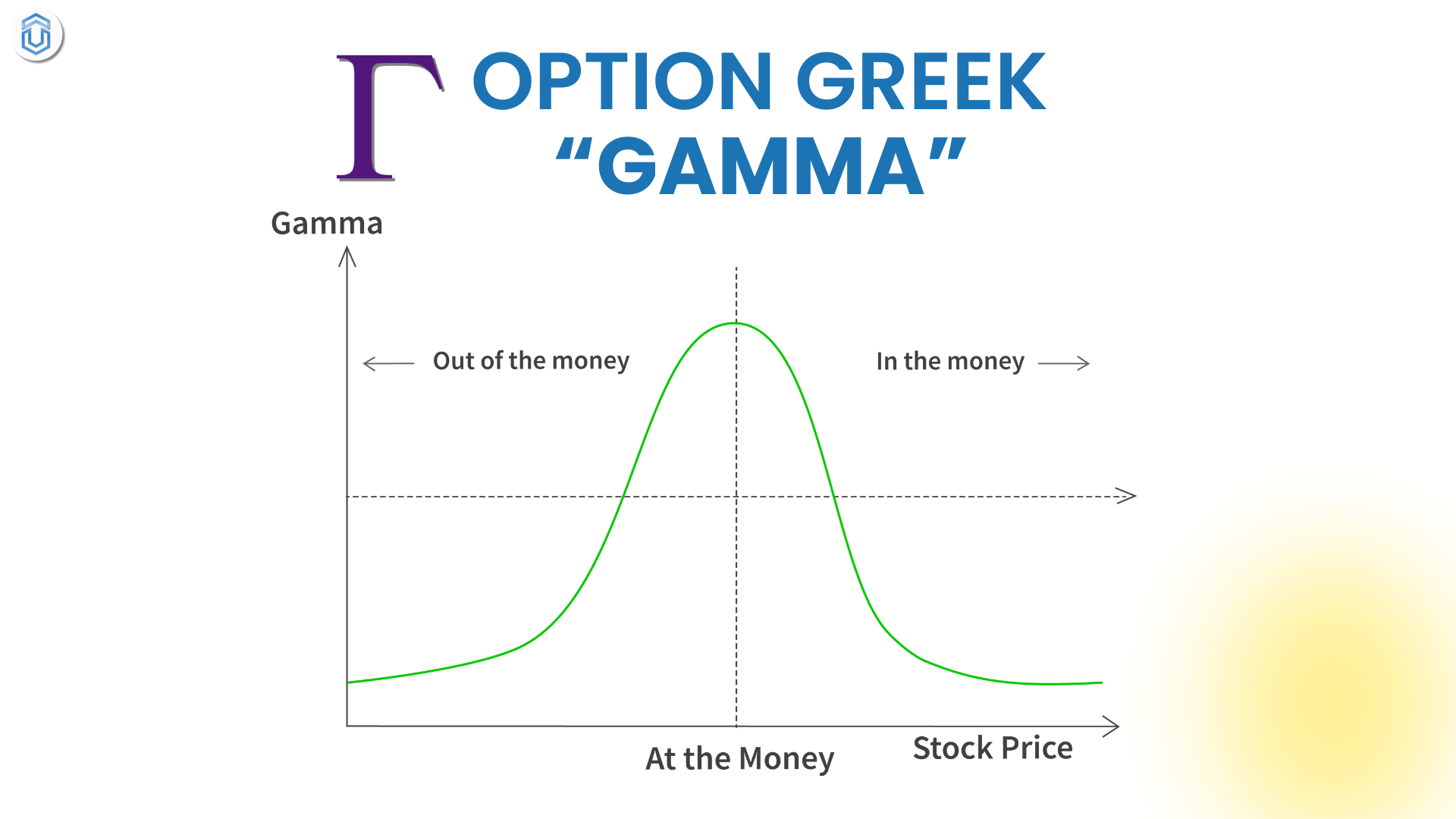
Gamma is the derivative of Delta. While Delta tells you how much an option’s price will change with a ₹1 move in the underlying asset, Gamma tells you how much Delta itself will change when the underlying asset moves by ₹1.
Gamma helps to understand the stability of Delta. If Gamma is high, Delta will change significantly for small price movements in the underlying asset, making the option more sensitive and less predictable. If Gamma is low, Delta will remain more stable.
Gamma is always positive for both call and put options.
Gamma is highest for options that are near the money (ATM), and it decreases as the option becomes more deeply in-the-money (ITM) or out-of-the-money (OTM).
As expiration approaches, Gamma increases, especially for at-the-money options. This means that the option becomes more sensitive to price changes in the underlying asset as time runs out.
Example:
Let’s say you hold a call option for a stock, and you know the following:
The Delta of your call option is 0.50, meaning the option price will increase by ₹0.50 for every ₹1 increase in the stock price.
The Gamma of the same option is 0.10, meaning if the stock price increases by ₹1, the Delta will increase by 0.10. So, if the stock moves up by ₹1, the new Delta will be 0.60 (0.50 + 0.10).
If the stock price increases by another ₹1, the Delta will increase again (since Gamma is positive), making the option more sensitive to price movements as the stock continues to rise.
What is Theta in Option Greeks:
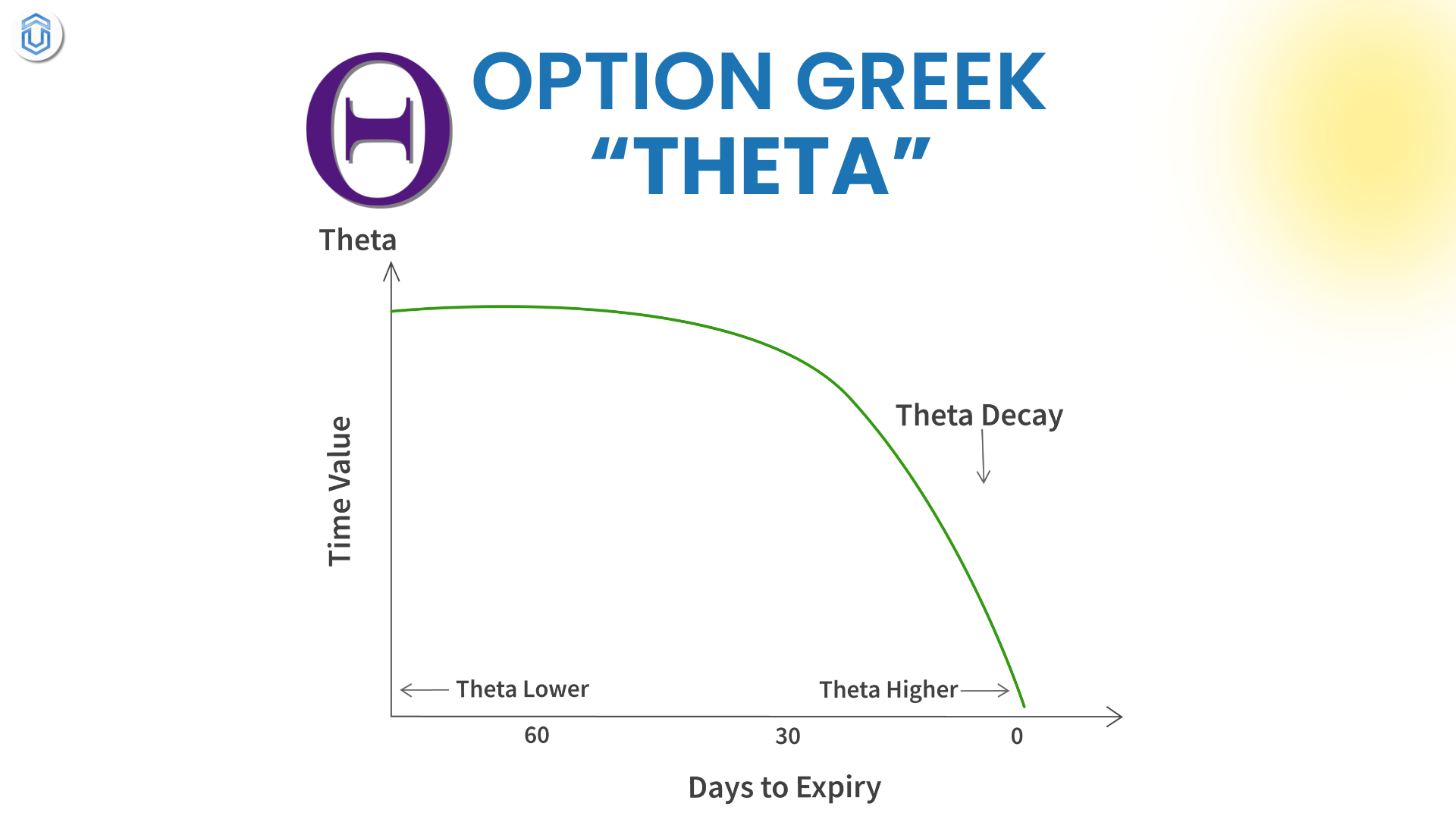
Theta represents the amount an option’s price will decrease per day as time passes, with all other factors (such as the price of the underlying asset and volatility) remaining constant.
The value of an option is made up of intrinsic value (if the option is in-the-money) and time value. As expiration approaches, the time value of an option shrinks, which is known as time decay. Theta measures this effect.
For both call and put options, Theta is generally negative. This means that options lose value as time passes.
The rate of time decay is usually more pronounced for options that are at-the-money (ATM) or out-of-the-money (OTM) because these options have less intrinsic value and more time value. In-the-money (ITM) options decay more slowly since they have intrinsic value.
As expiration nears, the impact of Theta increases. For example, Theta tends to accelerate as the option gets closer to expiration, especially for at-the-money options. This means that the option loses value faster as time runs out.
Option buyers (long positions) are negatively affected by Theta because their options lose value as time passes. This is why option buyers need the underlying asset to make significant moves in their favor within a short time frame.
Option sellers (short positions) benefit from Theta because they collect premium as the option loses time value. This is why selling options (especially near expiration) can be a profitable strategy if the market remains stable.
Example:
Imagine you hold a call option on a stock with a strike price of ₹500. The stock is currently trading at ₹510, and the option has a Theta of -0.05. This means that the option will lose ₹0.05 in value for every day that passes, assuming the stock price and other factors remain the same.
If the option has 30 days until expiration, the total time decay would be approximately ₹1.50 (30 days × ₹0.05/day). As the option nears expiration, Theta will accelerate, causing the time decay to become more pronounced.
What is Vega in Option Greeks:
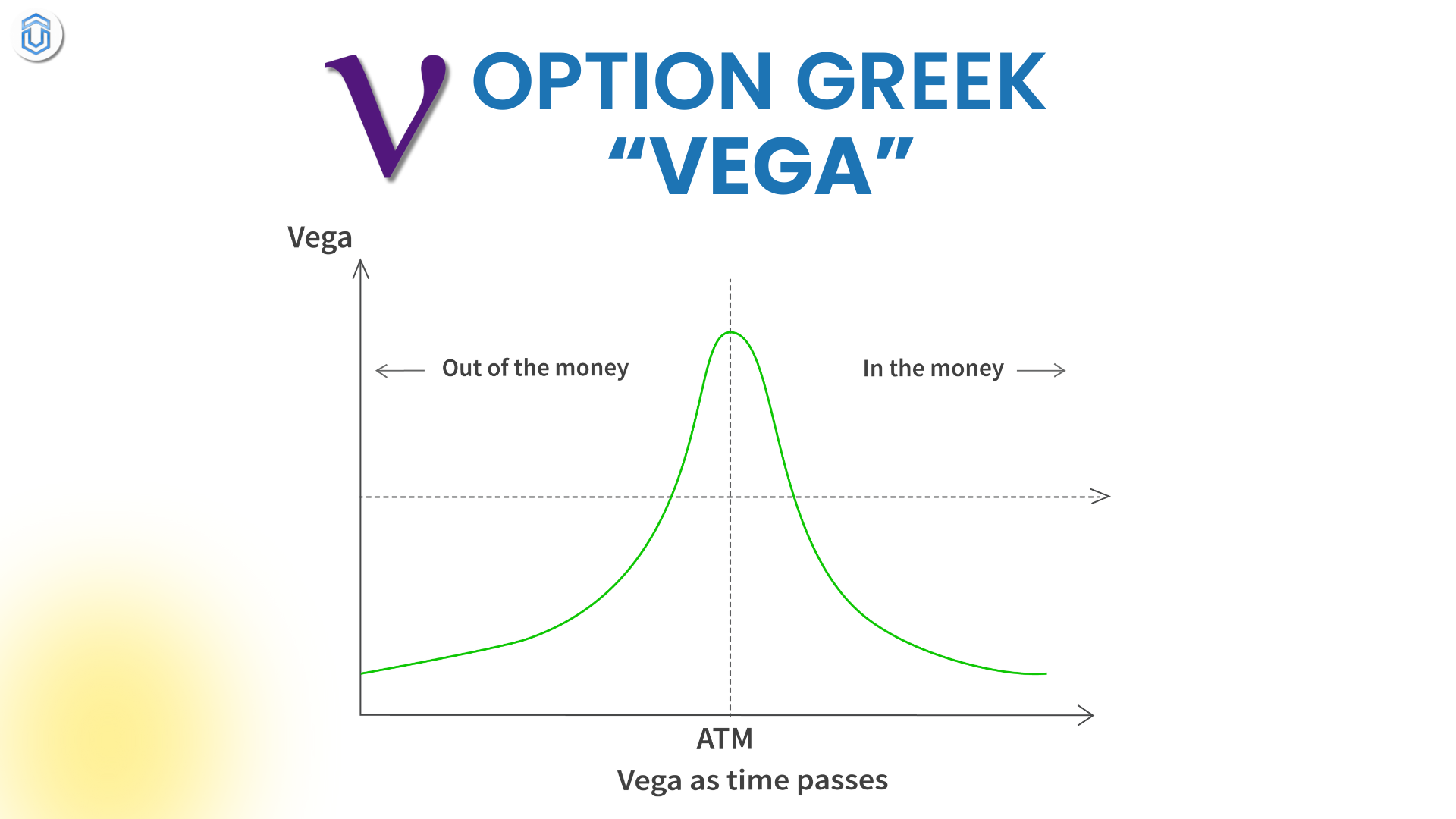
Vega (V) is a measure of an option’s sensitivity to changes in the volatility of the underlying asset. Specifically, Vega tells you how much the price of an option is expected to change for each 1% change in the implied volatility (IV) of the underlying asset, while keeping other factors like the price of the underlying asset and time to expiration constant.
Implied volatility (IV) refers to the market’s expectations of how much the underlying asset is likely to fluctuate in the future. If volatility increases, options (both calls and puts) generally become more expensive because higher volatility increases the potential for larger price movements.
Conversely, if volatility decreases, options tend to become cheaper, as the potential for large price swings is seen as lower.
Positive Vega: When implied volatility increases, the value of options (both call and put) tends to increase, and when volatility decreases, option prices tend to decrease.
Vega measures this change. A Vega of 0.10 means that if the implied volatility of the underlying asset increases by 1%, the option’s price will increase by ₹0.10 per share.
At-the-money (ATM) options have the highest Vega because they have the most time value and are most sensitive to changes in volatility.
In-the-money (ITM) and out-of-the-money (OTM) options have lower Vega. However, this is still important, especially for options with longer expirations, as their time value is more influenced by volatility.
Example:
Let’s say you have a call option for a stock with a strike price of ₹500, and the current implied volatility (IV) is 20%. The Vega of this option is 0.25.
If the implied volatility increases from 20% to 21%, the option price will increase by ₹0.25 for each share. So, if the option was priced at ₹5.00 before the volatility change, it will now be priced at ₹5.25 (assuming all other factors remain the same).
Conversely, if implied volatility drops by 1%, the option’s price would decrease by ₹0.25, assuming all other factors remain unchanged.
What is Rho in Option Greeks:

Rho (ρ) is an Option Greek that measures an option’s sensitivity to changes in interest rates. Specifically, it tells you how much the price of an option is expected to change for a 1% change in interest rates, while keeping all other factors (like the price of the underlying asset, volatility, and time to expiration) constant.
Interest rates have an impact on the present value of an option’s future payoff. As interest rates increase, the present value of future cash flows (such as those associated with exercising an option) becomes more valuable.
This is particularly relevant for call options.
For put options, the opposite is true. When interest rates rise, the present value of the payoff from selling the underlying asset (as in a put option) decreases, making the option less valuable.
Call Options: When interest rates increase, the price of a call option typically increases. This is because higher interest rates raise the cost of carrying the underlying asset, which makes the right to buy it in the future more valuable.
Put Options: When interest rates increase, the price of a put option typically decreases. This is because higher interest rates reduce the present value of the future payoff from exercising the put option.
Rho is particularly important for currency options, as interest rate differentials between two currencies can significantly affect the value of the option. For example, in the foreign exchange market, higher interest rates in one country relative to another can cause changes in the value of currency options.
Example:
Let’s say you hold a call option for a stock with a strike price of ₹500. The price of the stock is ₹520, and the interest rate is currently 5%. The Rho of the call option is 0.05.
If the interest rate increases from 5% to 6%, the price of the call option will increase by ₹0.05 for each share of the underlying stock, assuming all other factors (like the stock price, volatility, and time to expiration) remain constant.
Similarly, if you held a put option, an increase in interest rates would likely decrease the option’s price.
Conclusion:
By mastering these option Greeks, traders can make better risk management and improve their trading strategies. Whether you’re an option buyer looking to capitalize on price movements or an option seller benefiting from time decay, a strong grasp of the Greeks allows for more precise and strategic trading.
Ultimately, understanding and using Option Greeks effectively is key to navigating the complexities of options trading and maximizing your chances of success in the market.




